Learn the Guess and Check Method
What is the Guess and Check math strategy?
The Guess and Check Math strategy is one of the first few Math Heuristics that is introduced to Primary 3 students.
Although some students may switch to more advanced techniques like the Assumption method in Primary 4, mastering this method is still going to be useful to those who don’t in their upper primary years.
The main idea behind the Guess and Check method is to guess the answer to a problem and then check if the answer fits the given scenario. If it doesn’t, we’ll adjust our guess accordingly until all conditions are met.
Here’s what we’re going to cover:
How does the Guess and Check Method work?
The Guess and Check problem solving strategy is a fairly easy way of solving problems. Think of it as a 3-step-approach:
1. Guess –> 2. Check –> 3. Repeat if needed
While we are guessing the numbers, we’ll need to learn how to make smart guesses. Knowing how to do that helps us minimize the number of guessing, making the process more efficient.
We’ll see how to do that in a while.
Examples of Guess and Check Questions
Here are some samples of how Guess and Check Math Questions can look like.
Can you figure out what they have in common?
Primary 3 and 4 Math:
There are 15 cats and birds in a park. There are 42 legs altogether.
How many cats are there?
Primary 5 and 6 Math:
Jay did 20 Math questions during his math practice. He received 5 marks for every correct answer and he got 2 marks deducted for every wrong answer. If Jay earned 35 experience points in total, how many questions did he answer wrongly?
How do we identify questions that use the Guess and Check Method?
If you looked carefully, both problems that you see above has a total that’s made up of 2 kinds of items. on top of that, we also have some information about each item and we need to find the number of one of those items.
Let’s use the lower primary math problem as an example and go through the Guess and Check method step by step.
Part A: How to build the Guess and Check table the right way
Before we start guessing and checking, it’s always a good habit to build a guess and check table so that we know exactly what to look out for and keep things organized.
Step 1: List the 2 items that is in the question
The first thing that we’ll want to do is to build our guess and check table is to think about what we want to solve for. This is the answer that we are going to guess and it goes into our first column. In our case, it’s going to be the number of cats.
Next, we’ll list the number of the second item, which happens to be the number of birds as shown below:
Step 2: List the common thing that the 2 items have
What do the cats and birds have in common? Legs.
So the number of cats’ legs and the number of birds’ legs go into another 2 columns.
Step 3: Add in what we need to check
Time to think about the relationship between the columns and how they help us check if the answer that we have guessed is correct.
For our answer to be right, the total number of legs that we have has to add up to 42 and the way that we calculate this is to add the number of cats’ legs to the number of birds’ legs.
Let’s add another column to include the total number of legs and because we are going to use this to check of our guess is correct, we are going to add in another special column called “Check” to help us keep track of our progress.
Is the Guess and Check Table really necessary?
When we are busy making guesses, it is easy to lose track of the numbers that we have tried along with their calculations. That’s where a guess and check table can really come in handy. Not only does a guess and check table help us organize our guesses in a neat visual way, it also prevents us from making careless mistakes.
How to use the Guess and Check method efficiently
As you might have guessed, guessing and checking comes with a lot of hits and misses.
Here’s the trick to keep our guesses to a minimal and make the guess and check method work better!
Step 1: Start with the middle number as your first guess
In our example, since we have 15 pets, half of 15 would be approximately 7 or 8 (not 7.5 because we can’t have half a pet). Let’s pick 7 as our guess.
Step 2: Filling up our guess and check table from left to right
Once we have our guess, it’s time to work through the columns of our guess and check table and decide if our guess is correct.
If we had 7 cats and each puppy has 4 legs, we are going to have 7 x 4 cats’ legs = 28 cats’ legs.
To find the number of birds, let’s subtract 7 from the total of 15 pets. This gives us 8 birds.
8 birds are going to have 8 x 2 birds’ legs, 16 legs in all.
Let’s check the total number of legs we have against what is given in the problem. When we add 28 and 16, we are going to get a total of 44 legs. However, this is more than the 42 legs that we are given in the problem. Let’s make a note of that under the “Check” column.
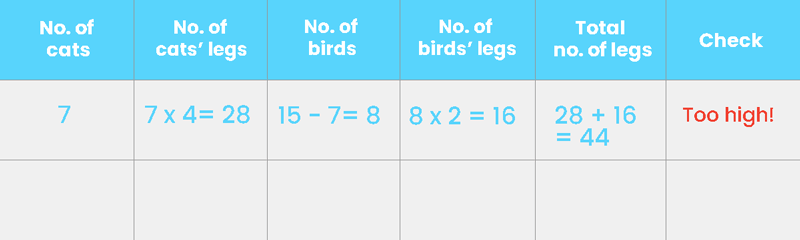
Step 3: Adjust our guess accordingly and check again
The next thing that we’ll want to do is to estimate how far our guess is to our target, and make a better guess.
Comparing our guess which resulted in 44 legs against the 42 legs that we want, we can tell that our guess is very close. Since we want to reduce the number of legs, should we increase or decrease our second guess?
Because the cats have more legs than birds and we want fewer legs, we’ll need to lower what we’ve guessed.
When we work systematically across our guess and check table, this happens to be the answer that we are looking for!
All it takes for us to get the correct answer are 2 guesses, and this definitely didn’t happen by chance.
When we made the first guess, it gave us some information about how far we are from the answer. This helped us make a better guess the second time. As you can see, we are making logical guesses instead of just guessing random numbers and trying our luck.
And that’s how you do the Guess and Check method!
Using the Guess and Check method is good when you are dealing with smaller numbers which are easier to work with. However, it does take practice to improve the accuracy of your guesses and some children may take a longer time to do the calculations in between, giving room to possible careless mistakes.
If you are looking for a faster alternative that involves fewer steps, you might want to check out the Assumption Method and see if that works better for you.
Need more examples?
Check out how this Math video on how to use the guess and check method to solve a Primary 3 question.
Like what you see? Subscribe to our Youtube channel for more Practicle Singapore Math videos!
