Learn the Assumption Method
What is the Assumption Method?
The Assumption Method (or the Supposition Method), is a Singapore Math problem-solving technique where you assume an extreme situation to solve a question. This method is often seen as a faster alternative as compared to the Guess and Check method that primary school students learn in Primary 3.
Here’s what we are going to cover:
Assumption vs Guess and Check – Which method is better for my child?
Before we answer that question, let’s first learn about the differences between these two approaches to problem solving.
Guessing and checking works for every kind of child. As long as a child has the time and patience, he/she will be able to guess the correct answer to the problem eventually. The number of guesses they need to make really depends on how strong their logic is and how lucky they are .
What about the assumption method?
Well, since this method only requires a child to make an assumption at the start, they won’t need to spend any unnecessary time guessing. All the time and energy saved can then be spent working their way towards the right solution.
The assumption method is definitely the faster and better choice, especially for children who are studying in upper primary (e.g Primary 4, 5 or 6). However, it may be a bit difficult for some children with a shaky Math foundation.
Fear not though, in the next section, Practicle is going to help you learn the assumption method easily!
Let’s start with the basics!
How does the assumption method work?
As mentioned earlier, we start by making an assumption about the problem. Most of the time, we are given two types of items and we want to make sure that we assume all the items to be one of the types.
For example, if we have apples and oranges, we’ll assume that all the fruits are apples or all of them are oranges. Either of these works.
Next, we’ll continue to make some deduction with what we have and compare our assumption with what we are given in the problem. Most of the time, it won’t be the same and we need to be able to come up with a logical explanation to help us find the answer.
Lost? Don’t worry! We’ll guide you through this step-by-step with a real word problem below.
Before we learn how to do the Assumption Method, let’s learn how to identify the kind of questions that we can solve with this method.
Examples of assumption method questions
Here are an example of a lower primary and upper primary Math problem sum questions that we can solve with the Assumption Method:
Primary 3 and 4 Math:
There are 15 mosquitoes and pest busters somewhere in Singapore. There are 54 legs altogether.
How many mosquitoes are there?
Primary 5 and 6 Math:
Iron Man made a total of 21 gadgets and masks for $3 340. It cost him $190 to make each gadget and $140 to make each mask.
How many masks did he make?
How do we identify questions that use the Assumption Method?
Check if your Math question contains:
- 2 types of items with a common property
- the total number of items and the total number of the common property
- an unknown number of each item
If it does, chances are, you are looking at an assumption question.
How to do the assumption method
Let’s use the Primary 4 Math question as an example.
The two types of items we have are mosquitoes and pest busters. The common property they have is legs.
The total number of items is 15. We have 15 mosquitoes and pest busters. What about the total number of legs? We are given that it is 54.. Since this is a Primary 4 Math problem, the P4 students are expected to be able to deduce that a mosquito has 6 legs while a pest buster has 2.
AS for the unknown number of each item, we are not given the exact number of mosquitoes, nor are we given the exact number of pest busters.
Steps for using the Assumption Method
Step 1:
ASSUME everything to be of the same type
Let’s assume that there are only pest busters.
Step 2:
MULTIPLY to find the total value
Next, calculate the total number of legs that we have.
No. of legs of 1 pest buster x No. of pest busters in our assumption
= 2 x 15
= 30
Looks like we have 30 legs.
However, when we look at the question, we are supposed to have 54 legs.
Step 3:
Find the DIFFERENCE (The gap between what we have in our assumption and what’s given in the problem)
54 – 30 = 24
Subtract the total number of legs in the problem from the total number of legs in our assumption.
Looks like we are short of 24 legs. What shall we do to get more legs then?
Remember the mosquitoes and pest busters that were mentioned in the question?
Since we have been working with only pest busters, it’s time to bring in the mosquitoes!
Step 4:
Find the EFFECT of replacing 1 item with the other
Subtract the number of legs of 1 pest busters from the number of legs of 1 mosquito.
6 – 2 = 4
This means that replacing 1 pest buster with 1 mosquito is going to increase the total number of legs by 4.
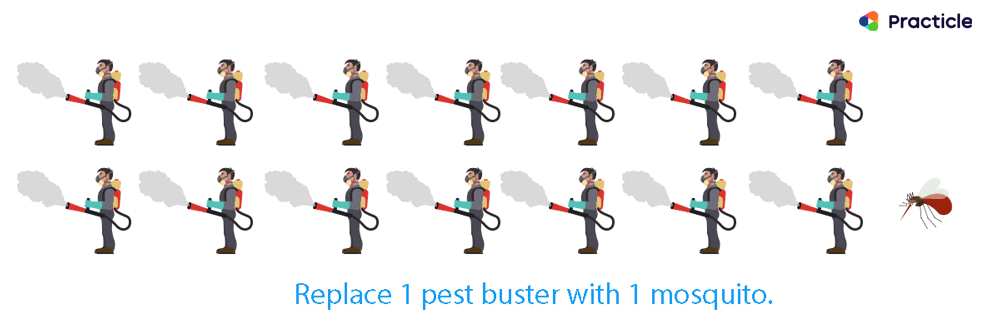
Step 5:
REPLACE subjects until we close the gap
Find the number of replacements we need to make so that we can close the gap of 24 legs.
24 / 4 = 6.
This tells us that we need to replace 6 pest busters with 6 mosquitoes.
That’s how we know we have 6 mosquitoes.
And that’s how you do the Assumption Method!
The next time you see Guess and Check questions for Primary 4, try using the Assumption Method instead of the Guess and Check method and see how much faster it takes to get the answer.
Need more examples?
Check out how we can use the assumption method for this p5 question!
Like what you see? Subscribe to our Youtube channel for more Practicle Singapore Math videos!